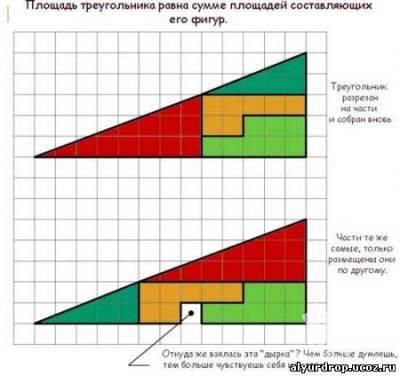
Площадь треугольника равна сумме площадей составляющих его фигур.
Треугольник разрезан на части и собран вновь.
Части те же самые, только размещены они по другому.
Откуда взялась эта "дырка"?

Площадь треугольника равна сумме площадей составляющих его фигур.
Треугольник разрезан на части и собран вновь.
Части те же самые, только размещены они по другому.
Откуда взялась эта "дырка"?
Комментариев: 48